DES 加密算法
对称加密算法:Data Encryption Standard
所谓对称加密算法,指的是加密和解密使用相同密钥的加密算法,而 Data Encryption Standard (数据加密标准),简称 DES,就是一种经典的对称加密算法。
DES 设计遵循 “香农准则”:
- 充分混乱:密钥、明文以及密文之间的依赖关系相当复杂。
- 充分扩散:密钥的每一位数字影响密文的许多位数字,明文的每一位数字也应影响密文的许多位数字。
DES 具有以下属性:
- 明文:M = { m1, m2, …, m64},64bits 信息。
- 密文:C = { c1, c2, …, c64},64bits 信息。
- 密钥:K = { k1, k2, …, k64},64bits,8为奇偶校验位,有效位 56 bits。
作为一个经典的加密算法,DES 在数十年经久不衰,本文则希望通过自顶向下的方法,探讨一下 DES 算法的具体原理。
另附:实现代码
一、DES 流程概览
在 DES 算法中,明文会被分组成 64 位一组。而每一组依次进入算法加密,因此在此我们只讨论 64位一组的加密。
1.1 总流程图
忽略一部分细节,DES 整个流程可用下图表示:
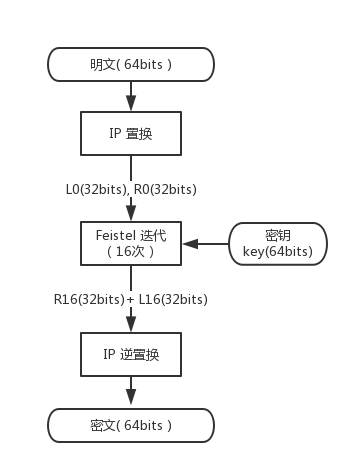
这个图只是 DES 算法的大体过程,忽略了很大一部分技术细节,那些省略的细节也会在第二、三部分进行详细讲解。现在看不懂这个图也没有关系,后文将逐渐展开。看完第一部分,请回到这里,看看能否对 DES 算法过程有一个宏观认识。
1.2 IP 置换 (初始置换)
s1. 明文为 64bits 的信息,按下表所示进行重新排列,即新的第 1 位为原来的第 58 位,新的第 2 位为原来的第 50 位……原有信息被打乱,这个过程称之为 IP 置换。
IP 置换表:
| 58 | 50 | 42 | 34 | 26 | 18 | 10 | 2 |
| 60 | 52 | 44 | 36 | 28 | 20 | 12 | 4 |
| 62 | 54 | 46 | 38 | 30 | 22 | 14 | 6 |
| 64 | 56 | 48 | 40 | 32 | 24 | 16 | 8 |
| 57 | 49 | 41 | 33 | 25 | 17 | 9 | 1 |
| 59 | 51 | 43 | 35 | 27 | 19 | 11 | 3 |
| 61 | 53 | 45 | 37 | 29 | 21 | 13 | 5 |
| 63 | 55 | 47 | 39 | 31 | 23 | 15 | 7 |
s2. 将经过 IP 置换重排后的信息分割成左右两部分 L[0] (32bits),R[0] (32bits)。
1.3 Feistel 迭代
IP 置换后的 L[0], L[1] 以及 64bits 的密钥 k 作为 Feistel 函数的输入,经过 16 次相同迭代,输出 L[16] (32bits) 和 R[16] (32bits)。
注:这部分细节将会在后续进行讲解。
1.4 IP 逆置换
将经过 Feistel 迭代的左右子串 L16,R16 按照 先右后左的 { R[16], L[16] } 顺序排列,经过 IP 置换的逆关系 IP逆 进行置换混淆,产生最后输出的密文。
IP 逆置换:
| 40 | 8 | 48 | 16 | 56 | 24 | 64 | 32 |
| 39 | 7 | 47 | 15 | 55 | 23 | 63 | 31 |
| 38 | 6 | 46 | 14 | 54 | 22 | 62 | 30 |
| 37 | 5 | 45 | 13 | 53 | 21 | 61 | 29 |
| 36 | 4 | 44 | 12 | 52 | 20 | 60 | 28 |
| 35 | 3 | 43 | 11 | 51 | 19 | 59 | 27 |
| 34 | 2 | 42 | 10 | 50 | 18 | 58 | 26 |
| 33 | 1 | 41 | 9 | 49 | 17 | 57 | 25 |
上面这三步就是整个 DES 算法的大体步骤。不过也正如同前面所说,这里省略了大量步骤,其中一个关键的步骤就是被一笔带过的 Feistel 迭代,下面也将会从这里开始讲起。
二、Feistel 轮函数详解
2.1 初始置换后的 16 次迭代
在 IP 置换(初始置换)后,经过重新排列混淆的 64bits 信息被分为左右两部分: L0(32bits), R0(32bits),这时候,它们要经过 16 次迭代,具体迭代过程如下图:
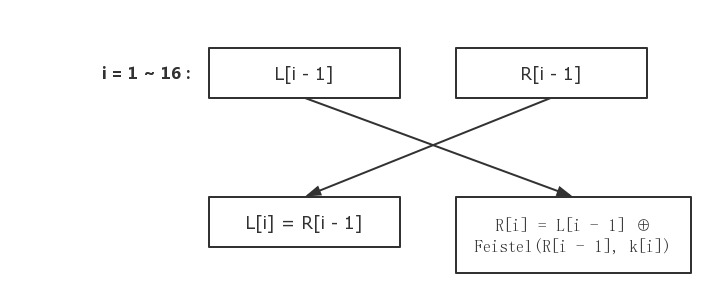
-
L[i]: 直接为上一层的 R[i - 1]
-
R[i]: 略微复杂一些,它是上一层的 L[i - 1] 与 Feistel 函数返回值的异或。
-
Feistel 函数: 接受两个参数:R[i - 1] 和 k[i] (后面详解),返回一个 32bits 的值。
2.2 Feistel 函数
-
参数:R[i - 1]: 32bits, k[i]: 48bits
-
返回:32bits
2.2.1 Feistel: 总流程
s1. 32bits 的 R[i - 1] 通过 E 扩展,变为 48bits 的 E(R[i - 1])。
s2. E(R[i - 1]) xor k[i],结果为 48bits。
s3. 将上述 xor 操作得到的结果分为 8 份,每份就是 6bits。
s4. 让第 i 份通过 S(i)Box,将会从 6bits -> 4bits。
s5. 将 8 份 4bits 数据组合成 32bits 的数据。
s6. 将上一步得到的 32bits 数据经过 P置换,然后输出 32bits 数据。
如下图:
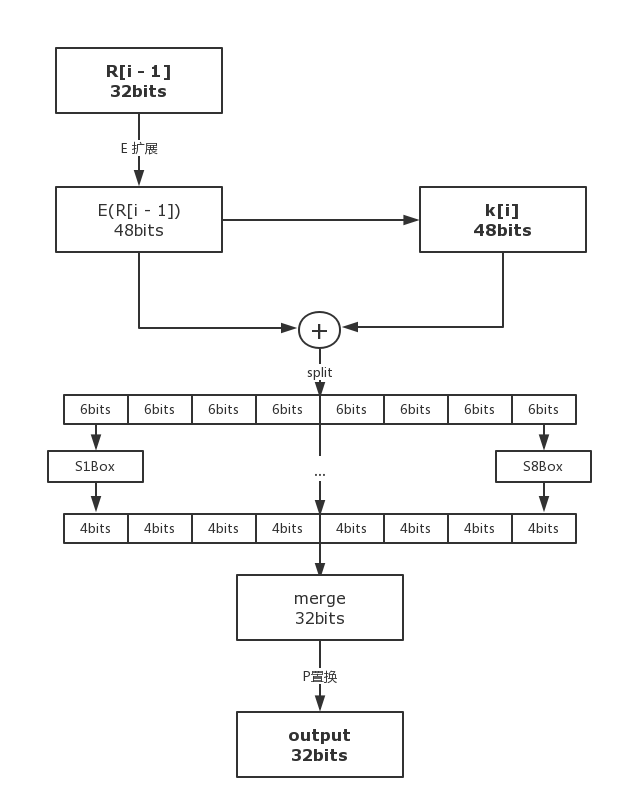
2.2.2 Feistel: E 扩展
Feistel 函数的一个步骤是:将 32bits 的 R[i - 1] 扩展成 48bits 的 E(R[i - 1]),这个过程不难理解。
首先,将 32bits 的 R[i - 1] 转化为 8 * 4 的矩阵。
现在,我们要扩展这个矩阵,使其扩展成 8 * 6 的矩阵,在首尾各增加一列:
利用原矩阵数据,依次循环向后扩展。
2.2.3 Feistel: S-Box
DES的核心是 S-Box,除此之外的计算是线性的。S-Box 作为该密码体制的非线性组件对安全性至关重要,但 S-Box 的设计原理至今未公布,是否存在隐藏陷门 ( Hidden Trapdoors ) 不得而知。
S-Box 的设计准则:
- S-Box 中的每一行是整数 0-15 的一个置换
- S-Box 不是它输入变量的线性或仿射函数
- S-Box 的输入端每改变1位至少要引起输出端改变 2 位
- S(X) 和 S(X + 001100) 至少有 2 位不同
- 对 6 位二进制串 X = x1x2x3x4x5x6,S(X) != S(X + {11x5x600})
- S-Box 的输入端保持任 1 位不变,则其它输入位的变化输出数字中 0 和 1 的总数近于相等。
S-Box 计算:
设S[i] 的6位输入为 { b1 b2 b3 b4 b5 b6 }
-
行号:r = ( b1 b6 )10
-
列号:c = ( b2 b3 b4 b5 )10
-
输出:(S[i])[r, c] 元素的值的二进制形式即为所要的 S[i] 的输出。
以 S1-Box 为例:
| 14 | 4 | 13 | 1 | 2 | 15 | 11 | 8 | 3 | 10 | 6 | 12 | 5 | 9 | 0 | 7 |
| 0 | 15 | 7 | 4 | 14 | 2 | 13 | 1 | 10 | 6 | 12 | 11 | 9 | 5 | 3 | 8 |
| 4 | 1 | 14 | 8 | 13 | 6 | 2 | 11 | 15 | 12 | 9 | 7 | 3 | 10 | 5 | 0 |
| 15 | 12 | 8 | 2 | 4 | 9 | 1 | 7 | 5 | 11 | 3 | 14 | 10 | 0 | 6 | 13 |
-
输入:{ b1 b2 b3 b4 b5 b6 } = 101100
-
行号:( b1 b6 )10 = (10)10 = 2
-
列号:( b2 b3 b4 b5 )10 = (0110)10 = 6
-
输出: S1[2, 6] = 2 = 0010
2.2.3 Feistel: P 置换
8 个 S-Box 最终会输出 8 组 4bits 的数据,将其合并为 32 bits,然后进行 P 置换,最后输出并参与 16 轮迭代。
P 置换表:
| 16 | 7 | 20 | 21 |
| 29 | 12 | 28 | 17 |
| 1 | 15 | 23 | 26 |
| 5 | 18 | 31 | 10 |
| 2 | 8 | 24 | 14 |
| 32 | 27 | 3 | 9 |
| 19 | 13 | 30 | 6 |
| 22 | 11 | 4 | 25 |
三、子密钥 k[i] 生成
在上述 Feistle 函数中,另一个参数就是 48bits 的 k[i],而 k[i] 便是通过密钥 k 生成的。这部分的生成只与密钥 k 相关,不依赖明文密文,所以这一步完全可以在整个算法第一步完成。
用下图表示子密钥 k[i] 生成过程:
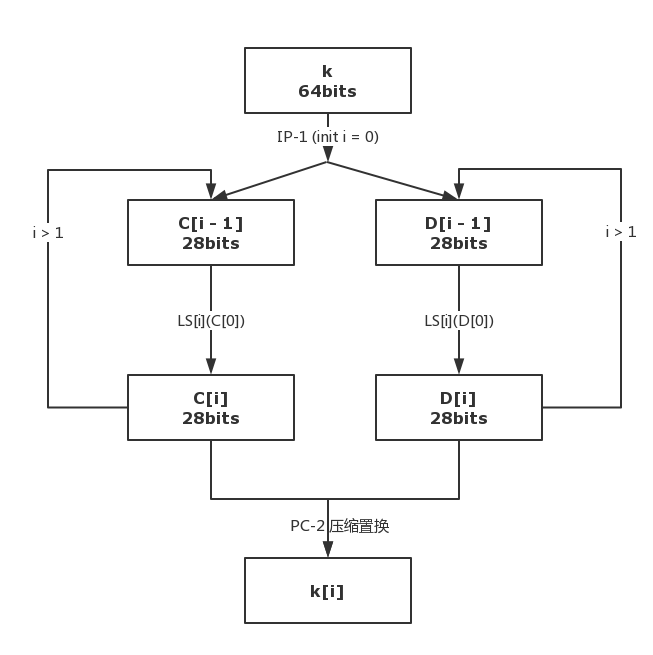
3.1 PC-1 置换
对 k 56bits 的非校验位进行 PC-1 置换混淆,得到左右各 28bits 两部分,记为 C[0], D[0]。
PC-1 置换表:
| 57 | 49 | 41 | 33 | 25 | 17 | 9 |
| 1 | 58 | 50 | 42 | 34 | 26 | 18 |
| 10 | 2 | 59 | 51 | 43 | 35 | 27 |
| 19 | 11 | 3 | 60 | 52 | 44 | 36 |
| 63 | 55 | 47 | 39 | 31 | 23 | 15 |
| 7 | 62 | 54 | 46 | 38 | 30 | 22 |
| 14 | 6 | 61 | 53 | 45 | 37 | 29 |
| 21 | 13 | 5 | 28 | 20 | 12 | 4 |
3.2 循环左移
从 i 开始,利用 C[i - 1], D[i - 1],计算 C[i], D[i]。
- C[i] = LS[i] (C[i - 1]) 和D[i] = LS[i] (D[i - 1])
- i = 1, 2, 9, 16 时:LS[i] (A) 表示 A 循环左移 1bit。
- i = others 时:LS[i] (A) 表示 A 循环左移 2bits。
可以用下表表示:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 |
3.3 PC-2 压缩置换
每一次循环,都拼接 C[i]D[i] 为 56bits 信息,进行 PC-2 压缩置换,压缩为 48bits,生成 k[i] 并输出。
PC-2 压缩置换表:
| 14 | 17 | 11 | 24 | 1 | 5 |
| 3 | 28 | 15 | 6 | 21 | 10 |
| 23 | 19 | 12 | 4 | 26 | 8 |
| 16 | 7 | 27 | 20 | 13 | 2 |
| 41 | 52 | 31 | 37 | 47 | 55 |
| 30 | 40 | 51 | 45 | 33 | 48 |
| 44 | 49 | 39 | 56 | 34 | 53 |
| 46 | 42 | 50 | 36 | 29 | 32 |
附:全部 S-Box
S1:
| 14 | 4 | 13 | 1 | 2 | 15 | 11 | 8 | 3 | 10 | 6 | 12 | 5 | 9 | 0 | 7 |
| 0 | 15 | 7 | 4 | 14 | 2 | 13 | 1 | 10 | 6 | 12 | 11 | 9 | 5 | 3 | 8 |
| 4 | 1 | 14 | 8 | 13 | 6 | 2 | 11 | 15 | 12 | 9 | 7 | 3 | 10 | 5 | 0 |
| 15 | 12 | 8 | 2 | 4 | 9 | 1 | 7 | 5 | 11 | 3 | 14 | 10 | 0 | 6 | 13 |
S2:
| 15 | 1 | 8 | 14 | 6 | 11 | 3 | 4 | 9 | 7 | 2 | 13 | 12 | 0 | 5 | 10 |
| 3 | 13 | 4 | 7 | 15 | 2 | 8 | 14 | 12 | 0 | 1 | 10 | 6 | 9 | 11 | 5 |
| 0 | 14 | 7 | 11 | 10 | 4 | 13 | 1 | 5 | 8 | 12 | 6 | 9 | 3 | 2 | 15 |
| 13 | 8 | 10 | 1 | 3 | 15 | 4 | 2 | 11 | 6 | 7 | 12 | 0 | 5 | 14 | 9 |
S3:
| 10 | 0 | 9 | 14 | 6 | 3 | 15 | 5 | 1 | 13 | 12 | 7 | 11 | 4 | 2 | 8 |
| 13 | 7 | 0 | 9 | 3 | 4 | 6 | 10 | 2 | 8 | 5 | 14 | 12 | 11 | 15 | 1 |
| 13 | 6 | 4 | 9 | 8 | 15 | 3 | 0 | 11 | 1 | 2 | 12 | 5 | 10 | 14 | 7 |
| 1 | 10 | 13 | 0 | 6 | 9 | 8 | 7 | 4 | 15 | 14 | 3 | 11 | 5 | 2 | 12 |
S4:
| 7 | 13 | 14 | 3 | 0 | 6 | 9 | 10 | 1 | 2 | 8 | 5 | 11 | 12 | 4 | 15 |
| 13 | 8 | 11 | 5 | 6 | 15 | 0 | 3 | 4 | 7 | 2 | 12 | 1 | 10 | 14 | 9 |
| 0 | 6 | 9 | 0 | 12 | 11 | 7 | 13 | 15 | 1 | 3 | 14 | 5 | 2 | 8 | 4 |
| 3 | 15 | 0 | 6 | 10 | 1 | 13 | 8 | 9 | 4 | 5 | 11 | 12 | 7 | 2 | 14 |
S5:
| 2 | 12 | 4 | 1 | 7 | 10 | 11 | 6 | 8 | 5 | 3 | 15 | 13 | 0 | 14 | 9 |
| 14 | 11 | 2 | 12 | 4 | 7 | 13 | 1 | 5 | 0 | 15 | 10 | 3 | 9 | 8 | 6 |
| 4 | 2 | 1 | 11 | 10 | 13 | 7 | 8 | 15 | 9 | 12 | 5 | 6 | 3 | 0 | 14 |
| 11 | 8 | 12 | 7 | 1 | 14 | 2 | 13 | 6 | 15 | 0 | 9 | 10 | 4 | 5 | 3 |
S6:
| 12 | 1 | 10 | 15 | 9 | 2 | 6 | 8 | 0 | 13 | 3 | 4 | 14 | 7 | 5 | 11 |
| 10 | 15 | 4 | 2 | 7 | 12 | 9 | 5 | 6 | 1 | 13 | 14 | 0 | 11 | 3 | 8 |
| 9 | 14 | 15 | 5 | 2 | 8 | 12 | 3 | 7 | 0 | 4 | 10 | 1 | 13 | 11 | 6 |
| 4 | 3 | 2 | 12 | 9 | 5 | 15 | 10 | 11 | 14 | 1 | 7 | 6 | 0 | 8 | 13 |
S7:
| 4 | 11 | 2 | 14 | 15 | 0 | 8 | 13 | 3 | 12 | 9 | 7 | 5 | 10 | 6 | 1 |
| 13 | 0 | 11 | 7 | 4 | 9 | 1 | 10 | 14 | 3 | 5 | 12 | 2 | 15 | 8 | 6 |
| 1 | 4 | 11 | 13 | 12 | 3 | 7 | 14 | 10 | 15 | 6 | 8 | 0 | 5 | 9 | 2 |
| 6 | 11 | 13 | 8 | 1 | 4 | 10 | 7 | 9 | 5 | 0 | 15 | 14 | 2 | 3 | 12 |
S8:
| 13 | 2 | 8 | 4 | 6 | 15 | 11 | 1 | 10 | 9 | 3 | 14 | 5 | 0 | 12 | 7 |
| 1 | 15 | 13 | 8 | 10 | 3 | 7 | 4 | 12 | 5 | 6 | 11 | 0 | 14 | 9 | 2 |
| 7 | 11 | 4 | 1 | 9 | 12 | 14 | 2 | 0 | 6 | 10 | 13 | 15 | 3 | 5 | 8 |
| 2 | 1 | 14 | 7 | 4 | 10 | 8 | 13 | 15 | 12 | 9 | 0 | 3 | 5 | 6 | 11 |