Gradient Descent ( 梯度下降 )

在之前的Logistic Regression 中，我们得到了整体的 Cost Function：

$\begin{aligned} J(\omega, b) & = \frac {1}{m}\sum_{i=1}^{m}L(\hat{y}^{(i)}, y^{(i)}) \\ &= -\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}\log \hat{y}^{(i)} + (1-y^{(i)})\log (1 - \hat{y}^{(i)})) \end{aligned}$

而我们要做的，就是最小化这个Cost Function。

算法原理

最简单的一个参数的例子说起

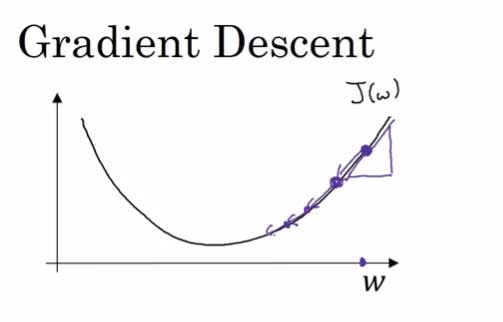
我们可以利用如下的公式：

$\omega := \omega - \alpha \frac {d J(\omega)}{d \omega}$

当 ω < 局部最优解的时候，导数 < 0，迭代让 ω 增大
当 ω > 局部最优解的时候，导数 > 0，迭代让 ω 减小

推广到多参数类型，ω 为 n 维向量，b 为实数，则：

$\omega := \omega - \alpha \frac {\partial J(\omega, b)}{\partial \omega}$ $b := b-\alpha \frac {\partial J(\omega, b)}{\partial b}$

Logistic Regression 迭代公式

刚好闲来无事，决定自己推一发这个公式，就当复习一下高数。

推导：

其中最重要的便是求出：

$\frac {\partial J(\omega, b)}{\partial \omega}$

设x(i)为2维向量：

$\begin{aligned} &\hat{y} = \sigma(z)=\frac{1}{1 + e^{-z}}\\\\ &z^{(i)} = \omega_1 x_1^{(i)} + \omega_2 x_2^{(i)} + b\\\\ &J(\omega, b) = -\frac {1}{m}\sum_{i=1}^{m}(y^{(i)}\log \hat{y}^{(i)} + (1-y^{(i)})\log (1 - \hat{y}^{(i)})) \end{aligned}$

微积分常识得到：

$\frac {\partial J(\omega, b)}{\partial \omega} = \frac {\partial J(\omega, b)}{\partial \hat{y}} \times \frac {\partial \hat{y}}{\partial z} \times \frac {\partial z}{\partial \omega}$

依靠这个式子，下面开始逐步化简。

第一项：

$\frac {\partial J(\omega, b)}{\partial \hat{y}} = -\frac {1}{m}\sum_{i=1}^{m}(\frac {y}{\hat{y}} - \frac{1 - y}{1 - \hat{y}})$

为了方便起见，先省略前面的求和符号,结尾处补上。

$\begin{aligned} &\frac {y}{\hat{y}} - \frac{1 - y}{1 - \hat{y}} \\\\ = & y + ye^{-z} + (y - 1)(e^z + 1) \\\\ = & y(2 + e^z + e^{-z}) - e^z - 1 \end{aligned}$

第二项：

$\frac {\partial \hat{y}}{\partial z} = \frac {1}{e^z + e ^{-z} + 2}$

第一项 × 第二项：

$\begin{aligned} &\frac {y(2 + e^z + e^{-z}) - e^z - 1}{e^z + e ^{-z} + 2} \\\\ = & y - \frac{e^z + 1}{e^z + e ^{-z} + 2} \\\\ = & y - \frac{e^{-z}(e^z + 1)}{(e^{-z} + 1)^2} \\\\ = & y - \frac{1 + e^{-z}}{(e^{-z} + 1)^2} \\\\ = & y - \frac{1}{e^{-z} + 1} \end{aligned}$

第三项：

$\frac {\partial z}{\partial \omega} = x$

补上求和符号，整体化简：

$\frac {\partial J(\omega, b)}{\partial \omega} = -\frac {1}{m}\sum_{i=1}^{m}(y - \frac{1}{e^{-z} + 1})x$

我们注意到，还可以化简为：

$\begin{aligned} &\frac {\partial J(\omega, b)}{\partial \omega}\\\\ = &-\frac {1}{m}\sum_{i=1}^{m}(y - \hat{y})x \\\\ = &\frac {1}{m}\sum_{i=1}^{m}(\hat{y} - y)x \end{aligned}$

结论：

得到 Logistic Regression 的 Gradient descent公式：

$\omega := \omega - \frac {\alpha}{m}\sum_{i=1}^{m}(\hat{y}^{(i)} - y^{(i)})x^{(i)}$

算法实现：

我们假设输入的训练样本 X 为 n * m 维矩阵，n 为feature 个数，m 为样例数。其中的 x(1), x(2) … 都是 n 维向量

$X = \left[ \begin{matrix} \vdots & \vdots & \vdots & \vdots \\ x^{(1)} & x^{(2)} & \dots & x^{(m)} \\ \vdots & \vdots & \vdots & \vdots \end{matrix} \right]$

初始化参数 n维向量 ω；实数 b

$\omega = \left[ \begin{matrix} \omega_1\\ \omega_2\\ \vdots\\ \omega_n\\ \end{matrix} \right]$

Step 1

$z = (\omega^T · X) + b$

Step 2

$\begin{aligned} &\hat{y} = \sigma(z)\\\\ &\frac {\partial J(\omega, b)}{\partial \omega} = \frac{1}{m} ( X · (\hat{y} - y)^T)\\\\ &\frac {\partial J(\omega, b)}{\partial b} = \frac{1}{m} (sum(\hat{y} - y)) \end{aligned}$

Step 3

$\begin{aligned} &\omega := \omega - \alpha \frac {\partial J(\omega, b)}{\partial \omega}\\\\ &b := b-\alpha \frac {\partial J(\omega, b)}{\partial b} \end{aligned}$

重复上述迭代。