Recursion Tree

在使用分治法( Divide and Conquer ) 来求解问题的过程中不可避免会用到递归( Recursion )，这给算法的复杂度分析带来了麻烦。但是幸运的是，递归树这种方法总能有用；不幸的是，它将会用到我们一个又爱又恨的符号，也就是 “点点点” ( … )

下面将会使用归并排序 ( Merge Sort ) 说明这种方法。

Merge Sort

主函数代码如下：

def merge_sort(nums):
    n = len(nums)
    if n < 2:
        return
    else:
        nums_left = merge_sort(nums[0 : n / 2])
        nums_right = merge_sort(nums[n / 2 : n])
        merge(nums_left, nums_right) #O(n)

Merge Sort 复杂度分析

• 设原问题的复杂度为 T(n)

• Merge 左右两个顺序序列复杂度为 O(n)

则：

递归树

建立递归树

我们设完成所有任务所需要的总步骤为 T(n) = 2 * T(n / 2) + cn:

显然，我们把最后一次 Merge 数据的步骤数设为 cn.

根据上述递推式建立递归树：

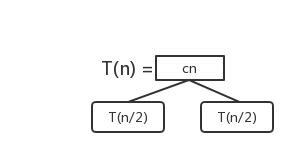
表示我们需要的总步骤为整个树的节点之和，即 T(n) = cn + 2 * T(n / 2)

而： T(n / 2) = (cn / 2) + 2 * T(n / 4)，所以我们继续补全递归树：

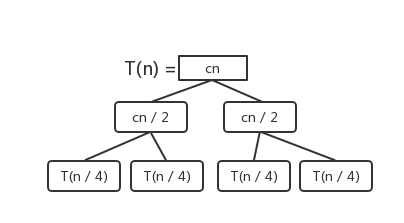
按照这个规则，最后到达最底部，整棵递归树完成：

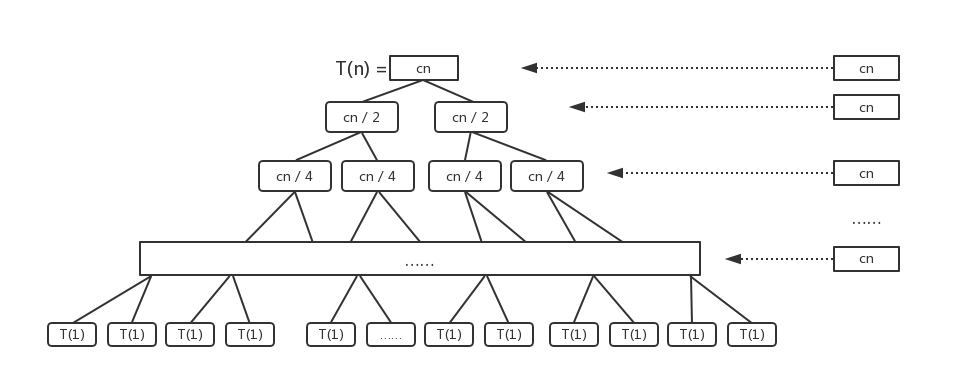
分析递归树

观察整个递归树，发现以下信息：

• 这颗递归树叶节点就是全部待排序的数字，为 n，最底层计算量为 O(n)。
• 递归树的高度为 log(n)
• 每层的计算量均为 cn

结论

可以计算 T(n) = log(n) * cn + O(n)

因为 cn = O(n)

因此:

所以 Merge Sort 复杂度为 O(nlogn)

同样的，如果递归式为 T(n) = 4T(n / 2) + O(n) 我们也可以利用递归树分析出 （式子中的相等指渐进意义下）:

因此，该算法复杂度为 O(n^2)